Fig (1):---
( each point (*) reoresents completely a parallel set of planes )
Since alk these points are parallel to b ,their normals lie in the plane of paper . To locate the points we have priceeded as followes:--
(1) :-- The normal to each plane from a common origin is drawn.
(2):-- A point on the normal at a distance from the origin equal to 1/d(hkl) has been placed.
Indeed the collection of such points form a lattice array . This array is called the reciprocal lattice, because distance in this lattice arr reciprocal to these in tge crystal.
Let us now define a reciprocal lattice vector . It is a vector whose magnitude is 1/d(hkl) and whose direction is parallel to the normal to the (hkl) planes.
The parallelopiped spanned by three non-coplanar reciprocal lattice vectors:-
######################
The Vector algebric analysis
######################
We shall now set up farmulae for finding the reciprocal lattice of a lattice algebrically.
Assume the primitive unit cell of volume V of the crystal lattice (fig2)
The volume V of the unit cell is equal to the area of the base (shaded), whose sides are b,c times the height of the cell, which is d(100)
Accordingly:-
These three vectors are chosen as the reciprocal translational vectorsb, for defining the 3 dim reciprocal lattice translational vector as:----
Reciprocal lattice translation vectors represent a simple relationship to the crystal translational vectors:---
relation 4 can be derived by forming the scalar product of both sides of 1st relation of 4 with b,c etc. Similarly eq7 can be derived by forming the scalar product of both sides of the first eq of 4 with a etc.
If a lattice is constructed using the reciprocal lattice vector (04), it follows that successive points in the direction represent successive submultiples h of the spacing of (100), in the b* direction , successive submultiples k of the spacing of (010) and in the c* direction , successive submultiples l of the spacing of (001)
That this is indeed so, is evident from 2.
Since:--
Therefore to reach any reciprocal lattice point hkl one gives h units along a*, k units along b*, and l units along c*.
Accordingly the reciprocal lattice vector can be written in vector notation as :---
1. The vector sigma(hkl) is normal to the crystal plane (hkl)
2. The length of the vector sigma (hkl) is equal to / d(hkl)
#######################
Proof of 1st property:--
########################
(a/h-b/k), (-a/h+c/l), (b/k-c/l) are the vectors lying in the plane (hkl)
Consider the product as:---
Eq 10 is the. required proof.
#######################
Proof of 2nd property
########################
In view of property 1st, n unit vector normal to plane (hkl) is parallel to sigma (hkl)
Thus:---
Or we can write as;---
Thus the reciprocal lattice spanned by eq 4 agrees with that traced out by the geometrical method.
######################
Unit cell
#######################
Volume of a unit cell of the reciprocal lattice is inversely proportional to the volume of a unit cell of the direct lattice.
Using eq 4, this becomes:--
-------- ---------- -----------










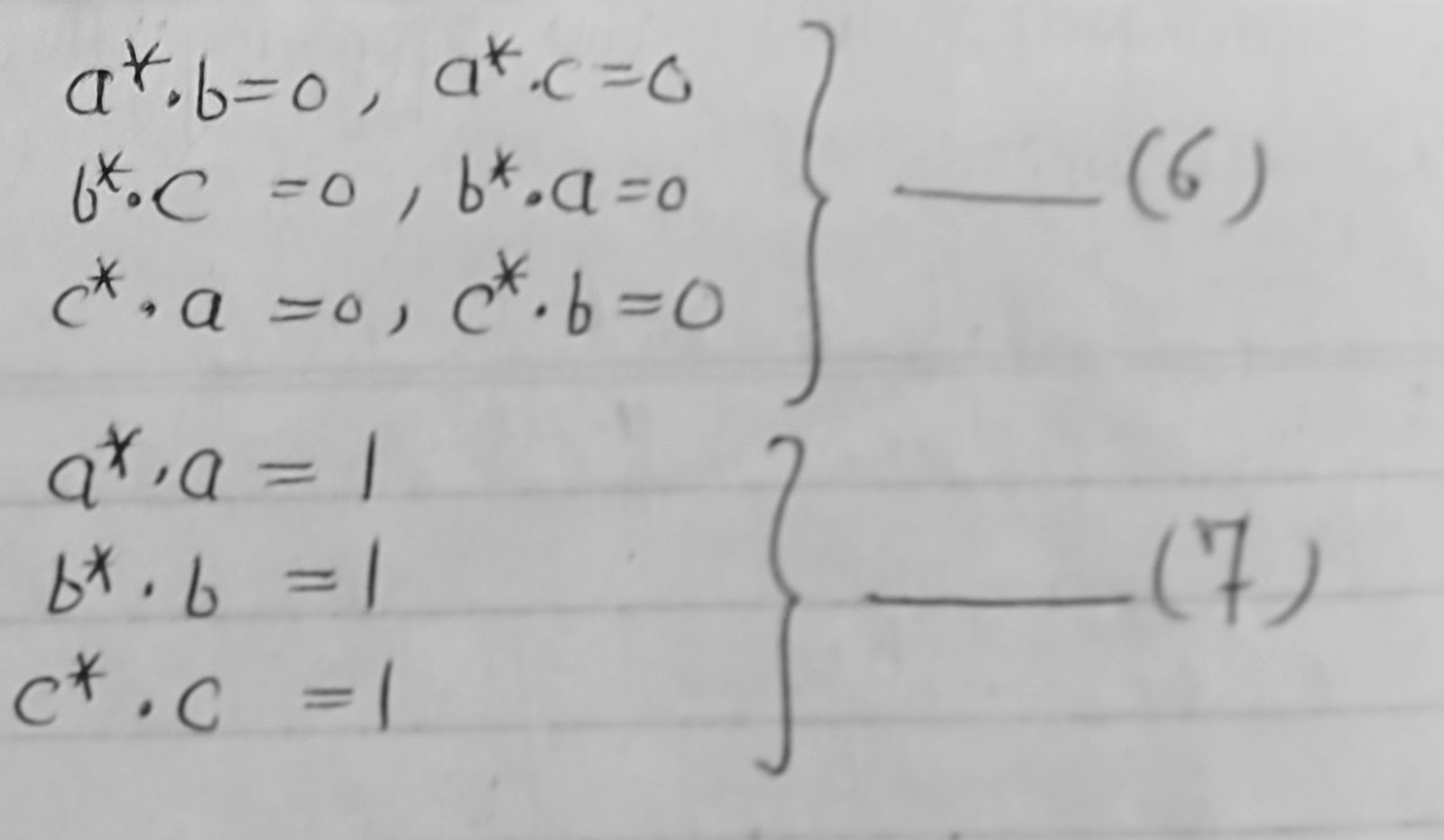







No comments:
Post a Comment